C2C #3: Game Trees

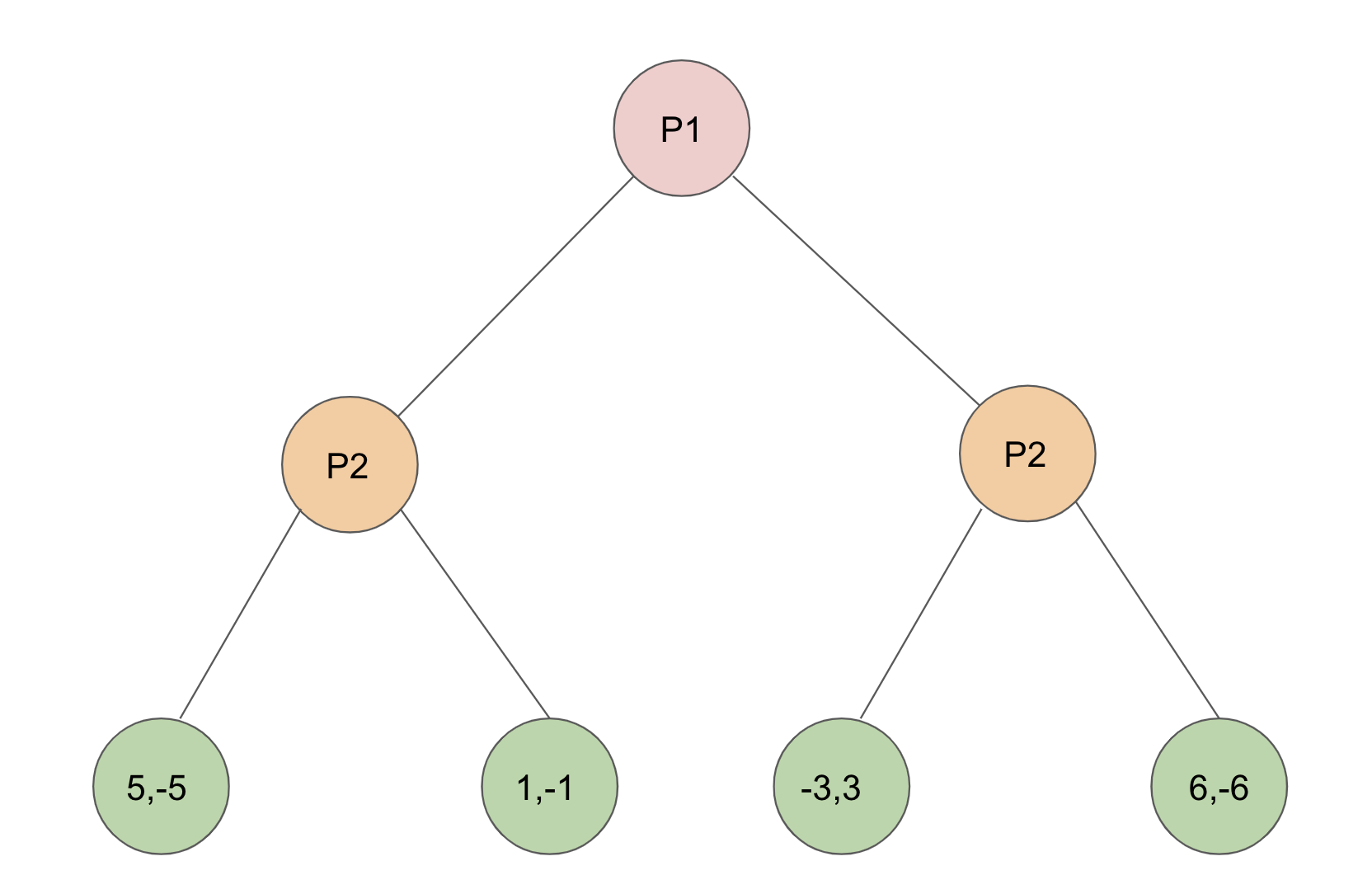
The standard way to solve a game tree like this is using backward induction, whereby we start with the leaves (i.e. the payoff nodes at the bottom) of the tree and see which decisions the last player, Player 2 in this case, will make at her decision nodes.

Player 2’s goal is to minimize the maximum payoff of Player 1, which in the zero-sum setting is equivalent to minimizing her own maximum loss or maximizing her own minimum payoff. This is equivalent to a Nash equilibrium in the zero-sum setting.

She picks the right node on the left side (payoff -1 instead of -5) and the left node on the right side (payoff 3 instead of -6).

These values are then propagated up the tree so from Player 1’s perspective, the value of going left is 1 and of going right is -3. The other leaf nodes are not considered because Player 2 will never choose those. Player 1 then decides to play left to maximize his payoff.

We can see all possible payouts, where the rows are P1 actions and the columns are P2 actions after P1 actions (e.g. Left/Left means P1 chose Left and then P2 also chose Left).

P1/P2	Left/Left	Left/Right	Right/Left	Right/Right
Left	5,-5	5,-5	1,-1	1,-1
Right	-3,3	-3,3	6,-6	6,-6

Note that Player 1 choosing right could result in a higher payout (6) if Player 2 also chose right, but a rational Player 2 would not do that, and so the algorithm requires maximizing one’s minimum payoff, which means Player 1 must choose left (earning a guaranteed value of 1).

By working backwards from the end of a game, we can evaluate each possible sequence of moves and propagate the values up the game tree.